Título: El estadígrafo Kendall y su aplicación. Un ejemplo práctico.
Autores: Dra.Noelia Barrueta Gómez.
DrC. Sergio Luis Peña Martínez.
DrC. Ernesto Fernández Sánchez.
Resumen: Dada la necesidad de incrementar el uso de métodos científicos durante el proceso de diseño, se ha propuesto explicar a través de un ejemplo de la práctica de esta disciplina, el uso del estadígrafo Kendall para la toma de decisiones, elemento en el que los diseñadores constantemente están inmersos durante su desempeño profesional y por qué no durante la etapa de su paso por la academia. Este proceso pasa por la planificación y realización de varias actividades que van a variar según el encargo de diseño y organizadas por fases y etapas según diferentes autores.
El diseño dejó de ser una disciplina intuitiva y casual, pasando a ser una disciplina científica y por ende deben involucrarse todos los autores del proceso docente en entenderlo y materializarlo en su desempeño con los estudiantes. Desde el momento en que el diseñador se enfrenta a diferentes problemas para darle una solución “óptima” ya está obligado a utilizar métodos que lo lleven de forma segura a esa solución, porque no debe ser producto del azar, sino que debe sustentarse en métodos que le permitan ahorrar recursos, obtener mejores prestaciones del producto, lograr materiales reciclables y que no sean nocivos al medio ambiente. Todo ello requiere de contar con herramientas matemáticas y con la consulta de quienes se consideren expertos en el campo del saber de qué se esté tratando, comenzando desde la búsqueda de información y recopilación de la más interesante, hasta la selección de la solución óptima. Para llegar a estas conclusiones, el diseñador no debe partir de su criterio personal, y más aún si su experiencia no es del todo amplia, para ello debe recurrir a probados métodos estadísticos, que de seguro le harán tomar el camino correcto respecto a una selección de alternativa consensuada previamente.
Por lo antes expuesto, el objetivo de este trabajo consiste en: Familiarizar a los diseñadores con la utilización de un estadígrafo que ayude a obtener consenso entre expertos sobre una cuestión determinada, para aplicarlo a sus proyectos de diseño cuando lo requieran.
Etapas del proceso de toma de decisiones.
Coeficiente de Kendall. Mide el grado de asociación entre varios conjuntos (k) de N entidades. Es útil para determinar el grado de acuerdo entre varios jueces, o la asociación entre variables.
Las etapas del proceso de toma de decisiones se resumen en:
1. Detección del problema.
2. Generación de alternativa.
3. Evaluación de las alternativas y selección de la mejor opción.
Como resultado del proceso se obtiene un plan de acción o proyecto que debe ser implementado y controlado con lo que se cierra el ciclo transformándose en el proceso de solución del problema.
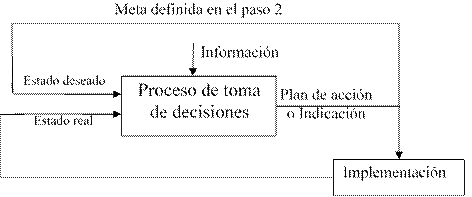
En cada etapa del proceso se identifican algunas técnicas aplicables. Estás técnicas se agrupan en:
• Métodos cuantitativos
• Métodos cualitativos
Las técnicas de consenso son métodos cualitativos que permiten la integración de los juicios de diferentes personas o instituciones tomando la decisión sobre la base del acuerdo de la mayoría. Se utilizan cuando:
• Las alternativas a evaluar son multifactoriales
• No existen posibilidades en el corto plazo de cuantificar la influencia de los factores en cada alternativa. Ejemplos
Elaboración del presupuesto para la Reparación Capital del ISDi en el 2021.
Selección de un Proyecto para Producir un producto de impacto en el mercado nacional.: ¿Qué alternativa es mejor: un mobiliario, una cafetera eléctrica, una cocina de inducción, un simulador de transporte, un vehículo eléctrico, una maquinaria para el corte de marabú, ¿un dispositivo para bajar de peso?
¿Qué elementos tuvieron en cuenta para decidir? ¿Todos tienen la misma importancia? Técnicas de consenso
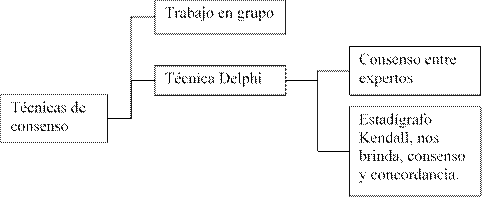
En pruebas estadísticas
En la prueba estadística el Coeficiente de Concordancia de Kendall (W), ofrece el valor que posibilita decidir el nivel de concordancia entre los expertos. El valor de W oscila entre 0 y 1. El valor de 1 significa una concordancia de acuerdos total y el valor de 0 un desacuerdo total. La tendencia a 1 es lo deseado pudiéndose realizar nuevas rondas si en la primera no es
alcanzada significación en la concordancia. Región crítica si χpract2 > χteor2 → hay consenso, estos dos valores no son difíciles de encontrar, en el ejemplo que pondremos a continuación se podrá ver claramente.
Importancia
Este método de pronóstico es importante porque brinda un modelo para ordenar las entidades de acuerdo a un consenso, cuando no hay un orden objetivo de las mismas.
Pasos para la aplicación de Kendall
1. Definir el problema.
2. Seleccionar los expertos, (Ei)
3. Elaborar los cuestionarios.
4. Definir los criterios, (Cj)
a. Por consenso sin identificación preliminar de los criterios.
b. Por consenso con identificación preliminar de los criterios.
c. Sin emplear el consenso a partir de estudios bibliográficos.
5. Consultar a los expertos sobre el orden de importancia. Aclarar que no deben tener ligas.
6. Conformar la matriz (Ei,Cj): Experto versus criterio.
a) debe asegurarse que 7 < E < 30. Esto lleva un proceso de selección donde clasifican los que posean coeficiente de competencia Kc > o igual de 0.7, esta metodología se explicará posteriormente con un ejemplo.
b) Calcular:
1.Suma de ranking → ∑rij , solo sumar cada columna.,
2.
Media → rij
= ∑∑C
rij
, se calcula la media dividiendo entre el total de criterios,
como se estudió en epígrafes anteriores, es el promedio.( Véase que son
medidas de tendencia central )
3.
Desviación media → ∑rij
− rij
, cada uno menos la media, aquí se encontrarán valores
negativos, es muy común.( También es una medida de la tendencia central de
determinados datos)
4.
Cuadrado de la desviación media → S=(∑rij
− rij
)2, por tanto
al elevarlos al cuadrado pasarán nuevamente a positivos, y es este valor el
fundamental para calcular el estadígrafo W, que es en definitiva quien nos da
el consenso o no entre los expertos.( Si observamos la fórmula 3 de la
desviación media, nos damos cuenta que la S, es esa misma magnitud, solo que al
cuadrado, con el objetivo de que los resultados sean todos positivos)
a. Por consenso sin identificación preliminar de los criterios.
b. Por consenso con identificación preliminar de los criterios.
c. Sin emplear el consenso a partir de estudios bibliográficos.
5. Consultar a los expertos sobre el orden de importancia. Aclarar que no deben tener ligas.
6. Conformar la matriz (Ei,Cj):
a. debe asegurarse que E > C, 7 < E < 30.
7. Calcular:
Suma de ranking → ∑rij
Media → rij
= ∑∑C rij
Desviación
media → ∑rij
− rij
Cuadrado
de la desviación media → S=(∑rij
− rij
)2
8. Calcular el estadígrafo. Aquí solo tener en cuenta si los criterios son menores de 7 o mayores de 7, porque se entra a diferentes tablas para determinar el estadígrafo Chi cuadrado.
![]() entonces S = S* y se calcula el
estadígrafo .
entonces S = S* y se calcula el
estadígrafo .
Si C > 7 se
calcula el estadígrafo 2 w ![]() S
S
Definir los valores de 2 práctico y 2 teórico
χpract2 = E(C −1)w
2 (α,C −1) χteor
Región crítica si χpract2 > χteor2 → hay consenso 9. Establecer la ponderación de los criterios.
w ![]() 1 E2(SC3 C)≤1----Observe que en esta
fórmula en el numerador se encuentra la S
1 E2(SC3 C)≤1----Observe que en esta
fórmula en el numerador se encuentra la S
Se definen los valores de χ 2 práctico y χ2 teórico, se comparan ambos valores y si el χpract2 , es mayor que el χteor2 , se considera que existe consenso entre los expertos.
Región crítica:
Planteamiento de la hipótesis:
H0: No existe concordancia entre los expertos.
H1: Existe concordancia entre los expertos.
Se rechaza la hipótesis nula H0, lo que significa que hay concordancia entre los expertos para un 95% de confianza, dado que el χpract2 es mayor que el χteor2 :
10.Todo lo anteriormente explicado, será demostrado a través de un ejemplo y usted verá cuan fácil resulta tanto los cálculos como la interpretación de los resultados.
Ejemplo relacionado con la Componente Laboral del Programa de Estudio de la carrera Diseño industrial.
Ejemplo (C > 7), Criterios a evaluar mayor que 7. Seguir la metodología explicada arriba.)
1. Definición del problema.
¿Qué criterios se deben tener en cuenta para seleccionar el Proyecto y alcanzar el éxito en la Práctica Laboral de estudiantes de diseño de 3er año?
2. Expertos: Colectivo de profesores de tercer año, Jefe de Departamento.
3. Criterios, observe que los criterios han sido seleccionados por profesores o personal que conoce los factores que inciden en la selección del Proyecto a realizar en las Prácticas laborales de alumnos de diseño de 3er año del ISDi y que influyen en el logro del éxito de la misma.
Estos criterios pueden ser redactados a partir de una lluvia de ideas que se realice con alumnos, profesores, donde vayan diciendo que elementos creen que ejercen influencia en lo antes planteado, de ahí, surgen los criterios que servirán para conformar la matriz que relaciona los criterios con la opinión de los expertos.
De esta forma, quedaron definidos 8 criterios que deberán ser evaluados por los expertos seleccionados por su coeficiente de competencia, es decir poseen experiencia, conocimiento del tema, llevan tiempo interactuando con lo relacionado a los proyectos de las Prácticas laborales etc.
|
C1 |
Condiciones de trabajo |
|
C2 |
Compromiso de los Tutores con el Tema a desarrollar |
|
C3 |
Importancia de la empresa en el sector |
|
C4 |
Ubicación de la empresa que garantice el fácil acceso. |
|
C5 |
Actualidad del tema y necesidad real de resolverlo |
|
C6 |
Posibilidad de continuar el Tema como Proyecto de Diploma |
|
C7 |
Imagen que proyecta la Empresa al público externo de la Empresa |
|
C8 |
Aplicabilidad del proyecto. |
4. Establecer el orden de importancia: 8 es el más importante y 1 el menos importante.
En esta matriz se han ordenado los criterios y los expertos, estableciendo el orden que cada experto le otorga a cada criterio según su importancia y su influencia en el problema a tratar.(Selección del proyecto a realizar en la Práctica Laboral).
|
Criterio |
E1 |
E2 |
E3 |
E4 |
E5 |
Suma |
Desv. |
(Desv)2 |
|
C1 |
1 |
3 |
2 |
1 |
1 |
8 |
-14.5 |
210.25 |
|
C2 |
8 |
7 |
8 |
8 |
7 |
38 |
15.5 |
240.25 |
|
C3 |
2 |
4 |
3 |
5 |
2 |
16 |
-6.5 |
42.25 |
|
C4 |
6 |
5 |
7 |
6 |
5 |
29 |
6.5 |
42.25 |
|
C5 |
3 |
1 |
1 |
2 |
3 |
10 |
-12.5 |
156.25 |
|
C6 |
7 |
8 |
5 |
7 |
8 |
35 |
12.5 |
156.25 |
|
C7 |
5 |
2 |
4 |
3 |
4 |
18 |
-4.5 |
20.25 |
|
C8 |
4 |
6 |
6 |
4 |
6 |
26 |
3.5 |
12.25 |
|
Media |
|
|
|
|
|
22.5 |
Total |
880 |
Observe como el E1, considera que el segundo criterio resulta ser el más importante, el que más influye, seguidamente, el C6, sigue en importancia, hasta llegar al menos importante o influyente, que para el experto E1,es el C1.
Como C > 7 entonces se aplica la prueba χ2 , chi cuadrado.( ver tabla segunda al final del texto, buscar el chi cuadrado teórico, según el nivel de significación y los grados de libertad que son un número menor que los expertos)
w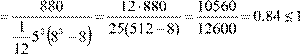
χpract2 = 5(8−1)⋅0.84 = 29.4
2 (0.05,7)=14.067 χteor
Región crítica:
Planteamiento de la hipótesis:
H0: No existe concordancia entre los expertos.
H1: Existe concordancia entre los expertos.
Se rechaza la hipótesis nula H0, lo que significa que hay concordancia entre los expertos para un 95% de confianza, dado que el Shi cuadrado práctico es mayor que el Shi cuadrado teórico:
Hay concordancia entre los expertos en el orden de importancia.
Significa que todos los expertos coinciden en 0,84 en que el orden de importancia es similar entre todos.
De esta forma se tabulan los datos con la ponderación.
Establecer la ponderación
|
Criterio |
Suma |
Desv. |
|
C1 |
8 |
-14.5 |
|
C2 |
38 |
15.5 |
|
C3 |
16 |
-6.5 |
|
C4 |
29 |
6.5 |
|
C5 |
10 |
-12.5 |
|
C6 |
35 |
12.5 |
|
C7 |
18 |
-4.5 |
|
C8 |
26 |
3.5 |
|
Total |
22.5 |
0 |
En la Tabla, según el mayor número de la suma será el criterio de mayor importancia y así sucesivamente hasta el menor.
|
Criterio |
Suma |
Desv. |
|
C2 |
38 |
15.5 |
|
C6 |
35 |
12.5 |
|
C4 |
29 |
6.5 |
|
C8 |
26 |
3.5 |
|
C7 |
18 |
-4,5 |
|
C3 |
16 |
-6.5 |
|
C5 |
10 |
-12.5 |
|
C1 |
8 |
-14.5 |
|
Promedio |
22.5 |
0 |
Con esto termina la aplicación de la técnica.
Es importante dejar claro que la forma de determinar el estadígrafo cambia, si por el contrario, la cantidad de criterios es menos que 7. A continuación se presenta un ejemplo: Si el problema es seleccionar una alternativa con esto no es suficiente. Hay que identificar las alternativas y evaluarlas. Para ello se debe aplicar la tabla de ponderación. Ejemplo 2 (igual al anterior, pero con C < 7)
|
C1 |
Condiciones de trabajo |
|
C2 |
Compromiso de los Tutores |
|
C3 |
Importancia de la empresa |
|
C4 |
Ubicación de la empresa |
|
C5 |
Importancia del Tema |
|
C6 |
Aplicabilidad del proyecto |
|
Criterio |
E1 |
E2 |
E3 |
E4 |
E5 |
Suma |
Desv. |
(Desv)[1] |
|
C1 |
1 |
2 |
2 |
1 |
1 |
7 |
-10.5 |
110.25 |
|
C2 |
6 |
5 |
5 |
6 |
5 |
27 |
9.5 |
90.25 |
|
C3 |
2 |
3 |
3 |
3 |
2 |
13 |
-4.5 |
20.25 |
|
C4 |
4 |
4 |
6 |
4 |
4 |
22 |
4.5 |
20.25 |
|
C5 |
3 |
1 |
1 |
2 |
3 |
10 |
-7.5 |
56.25 |
|
C6 |
5 |
6 |
4 |
5 |
6 |
26 |
8.5 |
72.25 |
|
|
Media |
17.5 |
Total |
369.5 |
||||
Como C < 7 verificar si se cumple que S > S*(5,6). ( Ver la primera tabla del final del documento y hacer coincidir la M de la tabla con los expertos y la N con los criterios)
369.5 > 182.4 por lo tanto S = 182.4. Sustituyendo en w se obtiene:
w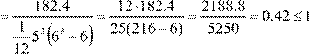
χpract2 = 5(6−1)⋅0.42 =10.5
No hay consenso.
En la Tabla de valores de críticos de S que se muestra seguidamente, M, es el número de expertos y N corresponde a los criterios.
En la Tabla de χ2, en la primera columna se entra por el número de expertos, que recordemos que es un número menor, porque los grados de libertad, se calculan como el número de expertos -1, por tanto 8 expertos, serían 7 grados de libertad y es con este número con el que se entra a la tabla., y en las filas se busca el nivel de significación, o sea el α= 0,05 en el caso del ejemplo con C>7.
Bibliografía
Florés, B., & Puig, A. (2008). ¿Hacia dónde se dirige la función de calidad?: la visión de expertos en un estudio Delphi. Revista Europea de Dirección y Economía de la Empresa, 18 (2), 13-38.
Eames, C., Daley, D., Hutchings, J., Whitaker, C.J., Bywater, T., Jones, K. & Hughes, J.C. (2010). The impact of group leaders’ behaviour on parents acquisition of key parenting skills during parent training. Behaviour Research and Therapy, 48, 1221-1226.
García, V., Aquino, S., Guzmán, A. & Medina, A. (2012). El uso del método Delphi como estrategia para la valoración de indicadores de calidad en programas educativos a Distancia.
Revista Calidad en la Educación Superior, 3 (1), 200 – 222.
González, I. & López, I. (2010). Validación y propuesta de un modelo de indicadores de evaluación de la calidad en la universidad. Revista Iberoamericana de Educación.
Landeta, J. (2006). Current validity of the Delphi method in social sciences. Technological Forecasting and Social Change, 73 (5), 467-482.
Rosas, A., Sánchez, J. & Chávez, M. (2012). La técnica Delphi y el análisis de la capacidad institucional de gobiernos locales que atienden el cambio climático. Política y Cultura, 38, 165-194.
Rowe, G. & Wright, G. (2012). The Delphi technique: Past, present, and future prospects
— Introduction to the special issue. Technological Forecasting and Social Change, 78 (9), 1487-
1498
Shapiro, C., Prinz, R. & Sanders, M. (2012). Facilitators and Barriers to Implementation of an Evidence-Based Parenting Intervention to Prevent Child Maltreatment: The Triple P-Positive Parenting Program. Child Maltreatment, 17 (1), 86-95.
Small, S., Cooney, S. & O’Connor, C. (2009). Evidence-Informed Program Improvement: Using Principles of Effectiveness to Enhance the Quality and Impact of Family-Based Prevention Programs. Family Relations, 58, 1-13.
Turner, K., Nicholson, J. & Sanders, M. (2011). The Role of Practitioner Self-Efcacy, Tra- ining, Program and Workplace Factors on the Implementation of an Evidence-Based Parenting Intervention in Primary Care. Journal of Primary Prevention, 32, 95–112. Turner, K. & Sanders, M. (2006). Dissemination of evidence-based parenting and fami- ly support strategies: Learning from the Triple P—Positive Parenting Program system approach. Aggression and Violent Behavior, 11, 176– 193